Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1.[1] Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and in everyday life (such as in counting). Numerous well-known quantities, such as π, e, and φ, are dimensionless.
Dimensionless quantities are often defined as products or ratios of quantities that are not dimensionless, but whose dimensions cancel out when their powers are multiplied. This is the case, for instance, with the engineering strain, a measure of deformation. It is defined as change in length over initial length but, since these quantities both have dimensions L (length), the result is a dimensionless quantity.
Contents |
Properties
- Even though a dimensionless quantity has no physical dimension associated with it, it can still have dimensionless units (i.e. not unitless). To show the quantity being measured (for example mass fraction or mole fraction), it is sometimes helpful to use the same units in both the numerator and denominator (kg/kg or mol/mol). The quantity may also be given as a ratio of two different units that have the same dimension (for instance, light years over meters). This may be the case when calculating slopes in graphs, or when making unit conversions. Such notation does not indicate the presence of physical dimensions, and is purely a notational convention. Other common dimensionless units are % (= 0.01), ‰ (= 0.001), ppm (= 10−6), ppb (= 10−9), ppt (= 10−12) and angle units (degrees, radians, grad). Units of amount such as the dozen and the gross are also dimensionless.
- The ratio of two quantities with the same dimensions is dimensionless, and has the same value regardless of the units used to calculate them. For instance, if body A exerts a force of magnitude F on body B, and B exerts a force of magnitude f on A, then the ratio F/f will always be equal to 1, regardless of the actual units used to measure F and f. This is a fundamental property of dimensionless proportions and follows from the assumption that the laws of physics are independent of the system of units used in their expression. In this case, if the ratio F/f was not always equal to 1, but changed if we switched from SI to CGS, for instance, that would mean that Newton's Third Law's truth or falsity would depend on the system of units used, which would contradict this fundamental hypothesis. The assumption that the laws of physics are not contingent upon a specific unit system is also closely related to the Buckingham π theorem. A formulation of this theorem is that any physical law can be expressed as an identity (always true equation) involving only dimensionless combinations (ratios or products) of the variables linked by the law (e. g., pressure and volume are linked by Boyle's Law – they are inversely proportional). If the dimensionless combinations' values changed with the systems of units, then the equation would not be an identity, and Buckingham's theorem would not hold.
Buckingham π theorem
Another consequence of the Buckingham π theorem of dimensional analysis is that the functional dependence between a certain number (say, n) of variables can be reduced by the number (say, k) of independent dimensions occurring in those variables to give a set of p = n − k independent, dimensionless quantities. For the purposes of the experimenter, different systems which share the same description by dimensionless quantity are equivalent.
Example
The power consumption of a stirrer with a given shape is a function of the density and the viscosity of the fluid to be stirred, the size of the stirrer given by its diameter, and the speed of the stirrer. Therefore, we have n = 5 variables representing our example.
Those n = 5 variables are built up from k = 3 dimensions which are:
- Length: L (m)
- Time: T (s)
- Mass: M (kg).
According to the π-theorem, the n = 5 variables can be reduced by the k = 3 dimensions to form p = n − k = 5 − 3 = 2 independent dimensionless numbers which are, in case of the stirrer:
- Reynolds number (a dimensionless number describing the fluid flow regime)
- Power number (describing the stirrer and also involves the density of the fluid)
Standards efforts
The International Committee for Weights and Measures contemplated defining the unit of 1 as the 'uno', but the idea was dropped.[2][3][4]
Examples
- Consider this example: Sarah says, "Out of every 10 apples I gather, 1 is rotten.". The rotten-to-gathered ratio is (1 apple) / (10 apples) = 0.1 = 10%, which is a dimensionless quantity.
- Another more typical example in physics and engineering is the measure of plane angles. An angle is measured as the ratio of the length of a circle's arc subtended by an angle whose vertex is the centre of the circle to some other length. The ratio, length divided by length, is dimensionless. When using radians as the unit, the length that is compared is the length of the radius of the circle. When using degree as the units, the arc's length is compared to 1/360 of the circumference of the circle.
- In the case of the dimensionless quantity π, being the ratio of a circle's circumference to its diameter, the number would be constant regardless of what unit is used to measure a circle's circumference and diameter (eg. centimetres, miles, light-years, etc), as long as the same unit is used for both.
List of dimensionless quantities
All numbers are dimensionless quantities. Certain dimensionless quantities of some importance are given below:
| Name | Standard symbol | Definition | Field of application |
|---|---|---|---|
| Abbe number | V | optics (dispersion in optical materials) | |
| Activity coefficient | γ | chemistry (Proportion of "active" molecules or atoms) | |
| Albedo |  |
climatology, astronomy (reflectivity of surfaces or bodies) | |
| Archimedes number | Ar | motion of fluids due to density differences | |
| Arrhenius number |  |
Ratio of activation energy to thermal energy[5] | |
| Atomic weight | M | chemistry | |
| Bagnold number | Ba | flow of bulk solids such as grain and sand.[6] | |
| Blowdown circulation number | BC | deviation from isothermal flow in blowdown (rapid depressurization) of a pressure vessel[7] | |
| Bejan number (thermodynamics) |
Be | the ratio of heat transfer irreversibility to total irreversibility due to heat transfer and fluid friction[8] | |
| Bejan number (fluid mechanics) |
Be | dimensionless pressure drop along a channel[9] | |
| Bingham number | Bm | 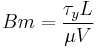 |
Ratio of yield stress to viscous stress[5] |
| Bingham capillary number | Bm.Ca | 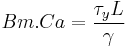 |
Ratio of yield stress to capillary pressure[10] |
| Biot number | Bi | surface vs. volume conductivity of solids | |
| Blake number | Bl or B | relative importance of inertia compared to viscous forces in fluid flow through porous media | |
| Bodenstein number | Bo | 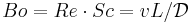 |
residence-time distribution |
| Bond number | Bo | capillary action driven by buoyancy [11] | |
| Brinkman number | Br | heat transfer by conduction from the wall to a viscous fluid | |
| Brownell–Katz number | combination of capillary number and Bond number | ||
| Capillary number | Ca | fluid flow influenced by surface tension | |
| Coefficient of static friction | 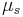 |
friction of solid bodies at rest | |
| Coefficient of kinetic friction | 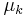 |
friction of solid bodies in translational motion | |
| Colburn j factor | dimensionless heat transfer coefficient | ||
| Courant–Friedrich–Levy number |  |
numerical solutions of hyperbolic PDEs [12] | |
| Damkohler number | Da |  |
reaction time scales vs. resonance time |
| Damping ratio | 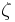 |
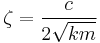 |
the level of damping in a system |
| Darcy friction factor | 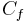 or or  |
fluid flow | |
| Dean number | D | vortices in curved ducts | |
| Deborah number | De | rheology of viscoelastic fluids | |
| Decibel | dB | ratio of two intensities, often sound | |
| Drag coefficient | 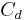 |
flow resistance | |
| Dukhin number | Du | ratio of electric surface conductivity to the electric bulk conductivity in heterogeneous systems | |
| Euler's number | e | mathematics | |
| Eckert number | Ec | convective heat transfer | |
| Ekman number | Ek | geophysics (frictional (viscous) forces) | |
| Elasticity (economics) | E | widely used to measure how demand or supply responds to price changes | |
| Eötvös number | Eo | determination of bubble/drop shape | |
| Ericksen number | Er | liquid crystal flow behavior | |
| Euler number | Eu | hydrodynamics (pressure forces vs. inertia forces) | |
| Excess temperature coefficient | Θr | 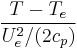 |
thermal and fluid dynamics[13] |
| Fanning friction factor | f | fluid flow in pipes [14] | |
| Feigenbaum constants |  |
chaos theory (period doubling) [15] | |
| Fine structure constant |  |
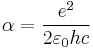 |
quantum electrodynamics (QED) |
| f-number |  |
optics, photography | |
| Foppl–von Karman number | thin-shell buckling | ||
| Fourier number | Fo | heat transfer | |
| Fresnel number | F | slit diffraction [16] | |
| Froude number | Fr | 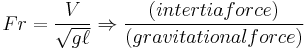 |
wave and surface behaviour |
| Gain | electronics (signal output to signal input) | ||
| Gain Ratio | system of representing bicycle gearing [17] | ||
| Galilei number | Ga | gravity-driven viscous flow | |
| Golden ratio |  |
mathematics and aesthetics | |
| Graetz number | Gz | heat flow | |
| Grashof number | Gr | free convection | |
| Gravitational coupling constant | 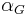 |
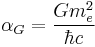 |
Gravitation |
| Hatta number | Ha | adsorption enhancement due to chemical reaction | |
| Hagen number | Hg | forced convection | |
| Hydraulic gradient | i | groundwater flow | |
| Jakob Number | Ja | 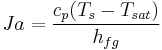 |
Ratio of sensible to latent energy absorbed during liquid-vapor phase change[18] |
| Karlovitz number | turbulent combustion turbulent combustion | ||
| Keulegan–Carpenter number | 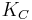 |
ratio of drag force to inertia for a bluff object in oscillatory fluid flow | |
| Knudsen number | Kn | ratio of the molecular mean free path length to a representative physical length scale | |
| Kt/V | medicine | ||
| Kutateladze number | K | counter-current two-phase flow | |
| Laplace number | La | free convection within immiscible fluids | |
| Lewis number | Le | ratio of mass diffusivity and thermal diffusivity | |
| Lift coefficient | 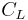 |
lift available from an airfoil at a given angle of attack | |
| Lockhart–Martinelli parameter | 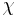 |
flow of wet gases [19] | |
| Love number | measuring the solidity of the earth | ||
| Lundquist number |  |
ratio of a resistive time to an Alfvén wave crossing time in a plasma | |
| Mach number | M | Ratio of current speed to the speed of sound, i.e. Mach 1 is the speed of sound, Mach 0.5 is half the speed of sound, Mach 2 is twice the speed of sound. | gas dynamics |
| Magnetic Reynolds number | 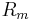 |
magnetohydrodynamics | |
| Manning roughness coefficient | n | open channel flow (flow driven by gravity) [20] | |
| Marangoni number | Mg | Marangoni flow due to thermal surface tension deviations | |
| Morton number | Mo | determination of bubble/drop shape | |
| Mpemba number | 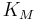 |
thermal conduction and diffusion in freezing of a solution[21] | |
| Nusselt number | Nu | 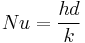 |
heat transfer with forced convection |
| Ohnesorge number | Oh | atomization of liquids, Marangoni flow | |
| Péclet number | Pe | 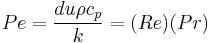 |
advection–diffusion problems; relates total momentun transfer to molecular heat transfer. |
| Peel number | adhesion of microstructures with substrate [22] | ||
| Perveance | K | measure of the strength of space charge in a charged particle beam | |
| Pi |  |
mathematics (ratio of a circle's circumference to its diameter) | |
| Poisson's ratio |  |
elasticity (load in transverse and longitudinal direction) | |
| Porosity |  |
geology | |
| Power factor | electronics (real power to apparent power) | ||
| Power number | 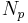 |
power consumption by agitators | |
| Prandtl number | Pr |  |
ratio of viscous diffusion rate over thermal diffusion rate |
| Pressure coefficient | 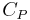 |
pressure experienced at a point on an airfoil | |
| Q factor |  |
describes how under-damped an oscillator or resonator is | |
| Radian | rad | measurement of angles | |
| Rayleigh number | Ra | buoyancy and viscous forces in free convection | |
| Refractive index | n | electromagnetism, optics | |
| Reynolds number | Re | 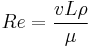 |
Ratio of fluid inertial and viscous forces[5] |
| Relative density | RD | hydrometers, material comparisons | |
| Richardson number | Ri | effect of buoyancy on flow stability [23] | |
| Rockwell scale | mechanical hardness | ||
| Rolling resistance coefficient | Crr | 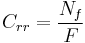 |
vehicle dynamics |
| Rossby number | 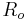 |
inertial forces in geophysics | |
| Rouse number | Z or P | sediment transport | |
| Schmidt number | Sc | fluid dynamics (mass transfer and diffusion) [24] | |
| Shape factor | H | ratio of displacement thickness to momentum thickness in boundary layer flow | |
| Sherwood number | Sh | mass transfer with forced convection | |
| Shields parameter | τ∗ or θ | threshold of sediment movement due to fluid motion | |
| Sommerfeld number | boundary lubrication [25] | ||
| Stanton number | St | heat transfer in forced convection | |
| Stefan number | Ste | heat transfer during phase change | |
| Stokes number | Stk or 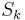 |
particle dynamics in a fluid stream | |
| Strain |  |
materials science, elasticity | |
| Strouhal number | St or Sr | nondimensional frequency, continuous and pulsating flow [26] | |
| Taylor number | Ta | rotating fluid flows | |
| Ursell number | U | nonlinearity of surface gravity waves on a shallow fluid layer | |
| Vadasz number | Va | 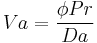 |
governs the effects of porosity  , the Prandtl number and the Darcy number on flow in a porous medium , the Prandtl number and the Darcy number on flow in a porous medium |
| van 't Hoff factor | i | quantitative analysis (Kf and Kb) | |
| Wallis parameter | J* | nondimensional superficial velocity in multiphase flows | |
| Weaver flame speed number | laminar burning velocity relative to hydrogen gas [27] | ||
| Weber number | We | multiphase flow with strongly curved surfaces | |
| Weissenberg number | Wi | viscoelastic flows [28] | |
| Womersley number |  |
continuous and pulsating flows [29] |
Dimensionless physical constants
Certain fundamental physical constants, such as the speed of light in a vacuum, the universal gravitational constant, and the constants of Planck and Boltzmann, are normalized to 1 if the units for time, length, mass, charge, and temperature are chosen appropriately. The resulting system of units is known as natural. However, not all physical constants can be eliminated in any system of units; the values of the remaining ones must be determined experimentally. Resulting constants include:
- α, the fine structure constant, the coupling constant for the electromagnetic interaction;
- μ or β, the proton-to-electron mass ratio, the rest mass of the proton divided by that of the electron. More generally, the rest masses of all elementary particles relative to that of the electron;
- αs, the coupling constant for the strong force;
- αG, the gravitational coupling constant.
See also
- Similitude (model)
- Orders of magnitude (numbers)
- Dimensional analysis
- Normalization (statistics) and standardized moment, the analogous concepts in statistics
- Buckingham π theorem
References
- ^ "1.8 (1.6) quantity of dimension one dimensionless quantity". International vocabulary of metrology — Basic and general concepts and associated terms (VIM). ISO. 2008. http://www.iso.org/sites/JCGM/VIM/JCGM_200e_FILES/MAIN_JCGM_200e/01_e.html#L_1_8. Retrieved 2011-03-22.
- ^ "BIPM Consultative Committee for Units (CCU), 15th Meeting" (PDF). 17–18 April 2003. http://www.bipm.fr/utils/common/pdf/CCU15.pdf. Retrieved 2010-01-22.
- ^ "BIPM Consultative Committee for Units (CCU), 16th Meeting" (PDF). http://www.bipm.fr/utils/common/pdf/CCU16.pdf. Retrieved 2010-01-22.
- ^ Dybkaer, René (2004). "An ontology on property for physical, chemical, and biological systems". APMIS Suppl. (117): 1–210. PMID 15588029. http://www.iupac.org/publications/ci/2005/2703/bw1_dybkaer.html.
- ^ a b c "Table of Dimensionless Numbers" (PDF). http://www.cchem.berkeley.edu/gsac/grad_info/prelims/binders/dimensionless_numbers.pdf. Retrieved 2009-11-05.
- ^ Bagnold number
- ^ Katz J. I. (2009). "Circulation in blowdown flows". J. Pressure Vessel Technology 131 (3): 034501. doi:10.1115/1.3110038.
- ^ Paoletti S., Rispoli F., Sciubba E. (1989). "Calculation of exergetic losses in compact heat exchanger passager". ASME AES 10 (2): 21–9.
- ^ Bhattacharjee S., Grosshandler W.L. (1988). "The formation of wall jet near a high temperature wall under microgravity environment". ASME MTD 96: 711–6.
- ^ German G., Bertola V. (2010). "The spreading behaviour of capillary driven yield-stress drops". Colloid Surface A 366: 18–26. doi:10.1016/j.colsurfa.2010.05.019.
- ^ Bond number
- ^ Courant–Friedrich–Levy number
- ^ Schetz, Joseph A. (1993). Boundary Layer Analysis. Englewood Cliffs, NJ: Prentice-Hall, Inc.. pp. 132–134. ISBN 013086885-X.
- ^ Fanning friction factor
- ^ Feigenbaum constants
- ^ Fresnel number
- ^ Gain Ratio - Sheldon Brown
- ^ Incropera, Frank P. (2007). Fundamentals of heat and mass transfer. John Wiley & Sons, Inc. p. 376.
- ^ Lockhart–Martinelli parameter
- ^ Manning coefficientPDF (109 KB)
- ^ Katz J. I. (2009). "When hot water freezes before cold". Am. J. Phys. 77: 27–29. Bibcode 2009AmJPh..77...27K. doi:10.1119/1.2996187. [1] Mpemba number
- ^ Peel number
- ^ Richardson number
- ^ Schmidt number
- ^ Sommerfeld number
- ^ Strouhal number
- ^ Weaver flame speed number
- ^ Weissenberg number
- ^ Womersley number
External links
- John Baez, "How Many Fundamental Constants Are There?"
- Huba, J. D., 2007, NRL Plasma Formulary: Dimensionless Numbers of Fluid Mechanics. Naval Research Laboratory. p. 23, 24, 25
- Sheppard, Mike, 2007, "Systematic Search for Expressions of Dimensionless Constants using the NIST database of Physical Constants."